Gelfond–Schneider constant

The Gelfond–Schneider constant is

2^{\sqrt{2}}=2.6651441426902251886502972498731\ldots

which was proved to be a transcendental number by Rodion Kuzmin in 1930.[1] In 1934, Aleksandr Gelfond proved the more general Gelfond–Schneider theorem,[2] which solved the part of Hilbert's seventh problem described below.

Contents

Properties

The square root of the Gelfond–Schneider constant is the transcendental number

\sqrt{2}^{\sqrt{2}}=1.6325269\ldots

This number raised to the power of √2 is equal to 2, which illustrates that an irrational number to the power of an irrational number can sometimes produce a rational number.

This same constant can be used to prove that "an irrational to an irrational power may be rational", even without first proving its transcendence. The proof proceeds as follows: either 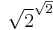\sqrt{2}^{\sqrt{2}} is rational, which proves the theorem, or it is irrational (as it turns out to be), and then 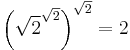\left(\sqrt{2}^{\sqrt{2}}\right)^{\sqrt{2}}=2 is an irrational to an irrational power that is rational, which proves the theorem. The proof is not constructive, as it does not say which of the two cases is true, but it is much simpler than Kuzmin's proof.

Hilbert's seventh problem

Main article: Hilbert's seventh problem

Part of the seventh of Hilbert's twenty three problems posed in 1900 was to prove (or find a counterexample to the claim) that ab is always transcendental for algebraic a ≠ 0, 1 and irrational algebraic b. In the address he gave two explicit examples, one of them being the Gelfond–Schneider constant 2√2.

In 1919, he gave a lecture on number theory and spoke of three conjectures: the Riemann hypothesis, Fermat's Last Theorem, and the transcendence of 2√2. He mentioned to the audience that he didn't expect anyone in the hall to live long enough to see a proof of this final result.[3] But the proof of this number's transcendence was published by Kuzmin in 1930,[1] well within Hilbert's own lifetime. Namely, Kuzmin proved the case where the exponent b is a real quadratic irrational, which was later extended to an arbitrary algebraic irrational b by Gelfond.

See also

References

  1. ^ a b R. O. Kuzmin (1930). "On a new class of transcendental numbers". Izvestiya Akademii Nauk SSSR, Ser. matem. 7: 585–597. 
  2. ^ Aleksandr Gelfond (1934). "Sur le septième Problème de Hilbert". Bull. Acad. Sci. URSS Leningrade 7: 623–634. 
  3. ^ David Hilbert, Natur und mathematisches Erkennen: Vorlesungen, gehalten 1919–1920.